Questão: Uma carreta sobe uma estrada cuja inclinação em relação à horizontal é de 30°, a uma velocidade de 40km/h. A força resistiva é igual a 0,75 do peso da carreta. Que velocidade teria a mesma carreta se descesse a estrada com a mesma potência?
Resposta:
Generalizando, vou chamar o ângulo de Θ e o coeficiente da orça resistiva de ψ.
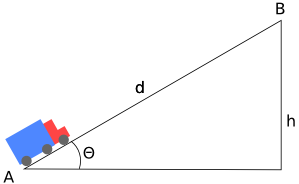
Figura 1 – A subida
Essa força resistiva não é exatamente o atrito, porque se fosse o atrito terÃamos de calcular as componentes do peso para descobrir a normal. O trabalho exercido por essa força resistiva é igual a força ψ·m·g vezes a distância d.
Na subida:
Ea=Eb
onde
- Ea = m·v²/2 + Em
- Eb = m·v²/2 + m·g·h + ψ·m·g·d
A carreta ira de um certo ponto A para um certo ponto B com uma mesma velocidade, a inércia pode cuidar disso. Mas a carreta precisa de alguma energia para converter em energia potencial gravitacional e na energia gasta pelo atrito. Essa energia vamos chamar de Em, a energia do motor. A carreta já parte com essa energia guardada para ser transformada em outras formas de energia. Podemos ver isso como o combustÃvel do veÃculo. Note que nenhuma energia aparece ou se perde.
Igualando as duas equações temos:
- m·v²/2 + Em = m·v²/2 + m·g·h + ψ·m·g·d
cortando a energia cinética dos dois lados e como h = d·senΘ:
- Em = m·g·d·senΘ + ψ·m·g·d
colocando d em evidência:
- Em = d·(m·g·senΘ + ψ·m·g)
A potência do motor na subida é dada pelo trabalho desenvolvido pelo motor dividido pelo tempo levado para subir do ponto A até o ponto B.
- Pm = Em/t
Como eu não tenho esse tempo eu posso dizer que o tempo é igual à distância dividida pela velocidade.
- Pm = Em/(d/v)
- Pm = Em·v/d
Substituindo Em:
- Pm = d·(m·g·senΘ + ψ·m·g)·v/d
- Pm = (m·g·senΘ + ψ·m·g)·v
- Pm = v·m·g·(senΘ + ψ)
Na descida:
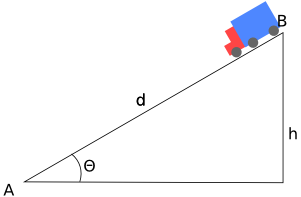
Figura 2 – A descida
Usando o mesmo raciocÃnio e notação da subida temos:
Ea=Eb
onde
- Ea = m·v²/2 + ψ·m·g·d
- Eb = m·v²/2 + m·g·h + Em
igualando as duas equações:
- m·v²/2 + ψ·m·g·d = m·v²/2 + m·g·h + Em
- ψ·m·g·d = m·g·h + Em
- Em = ψ·m·g·d – m·g·h
Como h = d·senΘ:
- Em = ψ·m·g·d – m·g·d·senΘ
- Em = d·m·g·(ψ – senΘ)
A potência do motor é dada pelo trabalho sobre o tempo:
- Pm = Em/t
Novamente não conhecemos o tempo mas sabemos que ele é a distância sobre a velocidade, que vou chamar de v linha para diferenciar da velocidade da carreta na subida:
- Pm = Em/(d/v’)
- Pm = Em·v’/d
Substituindo Em:
- Pm = d·m·g·(ψ – senΘ)·v’/d
- Pm = v’·m·g·(ψ – senΘ)
Como queremos que a potência na subida seja igual a potência na descida, igualamos as equações das potências:
- v·m·g·(senΘ + ψ) = v’·m·g·(ψ – senΘ)
- v·(senΘ + ψ) = v’·(ψ – senΘ)
- v’·(ψ – senΘ) = v·(senΘ + ψ)
- v’ = v·(senΘ + ψ) / (ψ – senΘ)
Note que nesse problema, a velocidade na descida só depende da velocidade na subida, o coeficiente da força resistiva e do ângulo Θ.
Calculando para v = 40km/h, ψ = 0,75, Θ = 30º e senΘ = 0,5.
- v’ = 40km/h·(0,5 + 0,75) / (0,75 – 0,5)
- v’ = 40km/h·1,25 / 0,25
- v’ = 200km/h